调制实验
一、 实验目的
1、了解调制在通信系统中的作用;
2、掌握常见的数字调制方法;
3、了解常见调制方法的解调方法。
二、 实验原理
1. 调制的基本概念:
射频信号被用来传递信息,信息有可能是音频,数据或者其他格式,该信息被调制(modulate)到载波信号上,并通过射频传送到接收器,在接收器端,信息从载波上分离出来,这个过程被称为解调(demodulation)。而载波本身并不带有任何信息。调制方法多种多样,简单的一般有幅度调制、频率调制和相位调制。
载波
无线通信的基础是载波,一般由在发射器部分产生,并不带有任何信息,在
接收器部分也作为不变的信号出现。
调幅
调幅通过调整信号幅度大小传递信息。最简单的调制是 OOK(on–off keying,开关键控),载波以开关的形式传递信息。在音频或其他领域应用更为常见的是,整个信号的幅度通过载波体现,这种调制方式被称为幅度调制(AM)。
调频
载波信号被调制后,频率会随着信号源电压变化,通过频率变化承载数据。FM 的一个重要的优势是不会受到源信号的电平变化的干扰,而且抗干扰的能力也强。
调相
相位调制是另一种广泛采用的调制技术,特别是在数据传输的应用中。因为相位和频率是相辅相成的(频变是相变的一种形式),两种调制方法可以用角度调制(angle modulation)来概括。
2、正交幅度调制:
而在移动通信系统中,广泛应用的数据传输方法是正交幅度调制(QAM)。被调制后输出信号在幅度和相位都有改变。因此不管幅度还是相位都会进行变化,所以可以看成是混合幅度和相位的调制。
下图 4bit 的数据可以分为一组并用图中的幅度和相位组合来表示,形成16QAM。
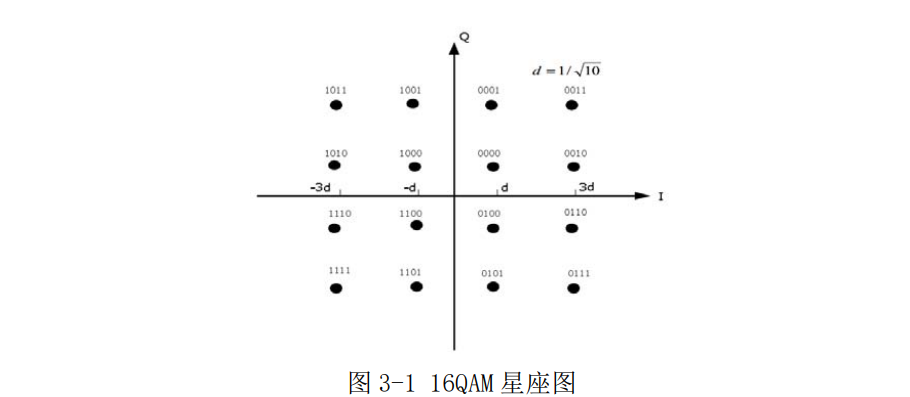
尽管 QAM 通过对幅度和频率的调制增加了传输效率,但比较容易受到噪声的影响,因为状态点距离很近,所以一个比较小的噪声就有可能将一个星座点移到错误的位置。第二个弱点也和幅度分量相关,相位调制和频率调制无需使用线性放大器;而 QAM 具有幅度分量,所以必须用线性放大。不幸的是,线性放大器一般功耗较高且效率不高。
3、正交幅度调制的解调:
定义一个含有 m 个比特的编码序列,在 i 时刻,该序列可表示为\{b_{i,1},b_{i,2},b_{i,3},……,b_{i,m}\}采用 M-QAM(M=2^m)调制方案,该序列可被映射为一个复值符号a(i)=a_l(i)+ja_Q(i),在星座图上可表示为点(a_l(i),a_Q(i)),其中a_l(i),a_Q(i)分别表示星座图的正交分量和同相分量。
用H_{ch}(i)表示信道频率响应,w(i)表示高斯白噪声,设其均值为0,方差为\frac{\sigma^2}{2}那么经 M-QAM 调制的信号经信道传输后,在接收端可表示为:
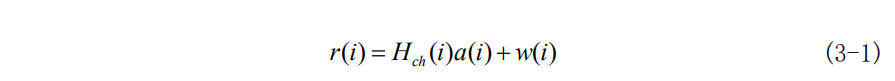
经过信道估计和均衡处理后,理想条件下的接收信号应该为:
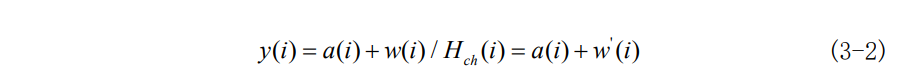
其中w'(i)仍为高斯白噪声,方差为\sigma'^2=\sigma^2/|H_{ch}(i)|^2。
最小欧氏距离软判决
由公式(3-2)可知,在a(i)=a的条件下,r(i)是一个复高斯随机变量,其概率表达式可表示为:
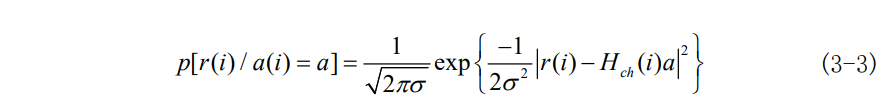
将r(i)=y(i)*H_{ch}(i)带入式中,可得:
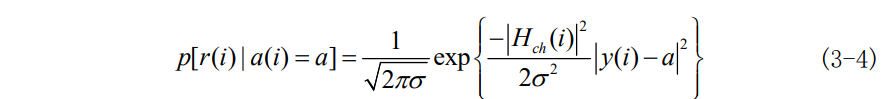
由于,b_{i,k}=0和b_{i,k}=1能够将星座图中的M个点分成两个集合,定义这两个集合为S_k^0(i),S_k^1(i)。由软信息的定义可知,相应比特的对数先验似然比 LLR 可表示为:
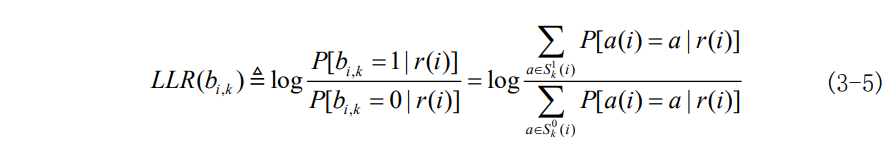
当LLR(b_{i,k})为正数时,表明b_{i,k}=1的概率大于b_{i,k}=0的概率,LLR(b_{i,k})值越大意味着b_{i,k}=1的后验概率越大。
在发送符号等概率的情况下,利用贝叶斯公式可以得到:
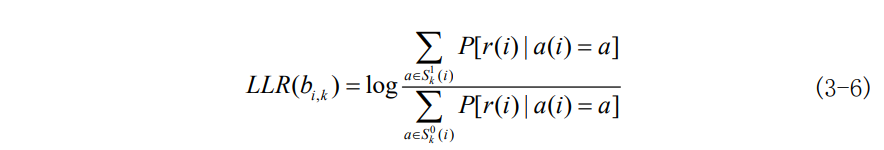
利用近似公式log\sum_{i} e^{x_i} \approx \max_{i}(x_i)将式子化简后可得:
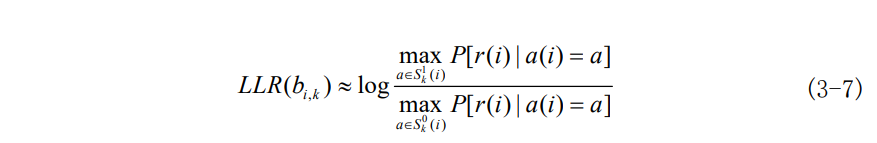
将公式(3-3)带入其中,可得LLR(b_{i,k})的近似计算公式为:
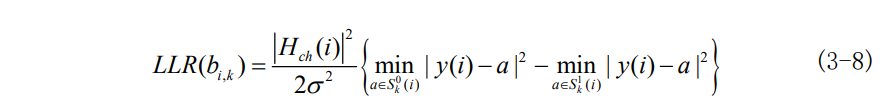
这种计算软信息的方法叫做最小欧氏距离软判决度量,其物理意义是分别
计算接收信号y(i)与星座图S_k^0(i),S_k^1(i)集合中所有点的距离,取两个最小的距离的差值。这种方法相对于直接计算 LLR 的方法省去了指数运算。我们将得到的软信息进行判决,就可以得到我们原始传输的信号比特了。
三、 实验仪器设备与材料
信号分布图
星座图
误码率记录仪
随机 M 进制序列模块
QAM 调制模块
加性高斯白噪声信道模块
多径干扰模块
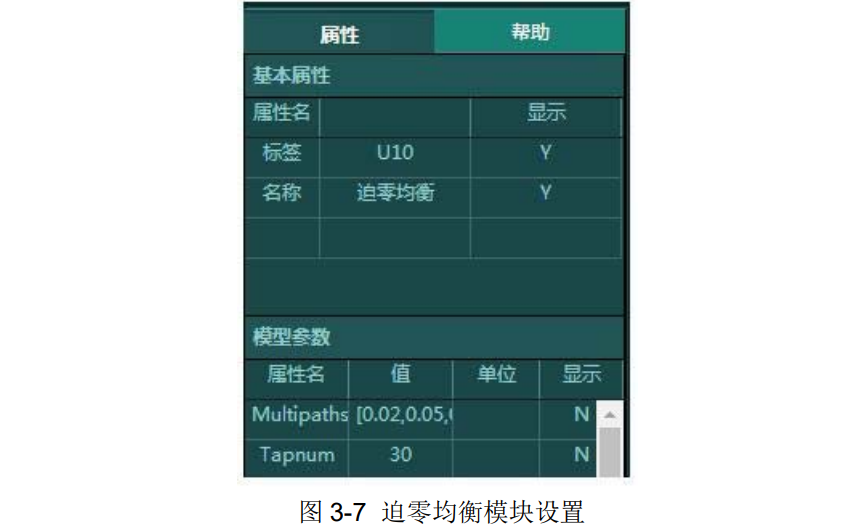
迫零均衡模块
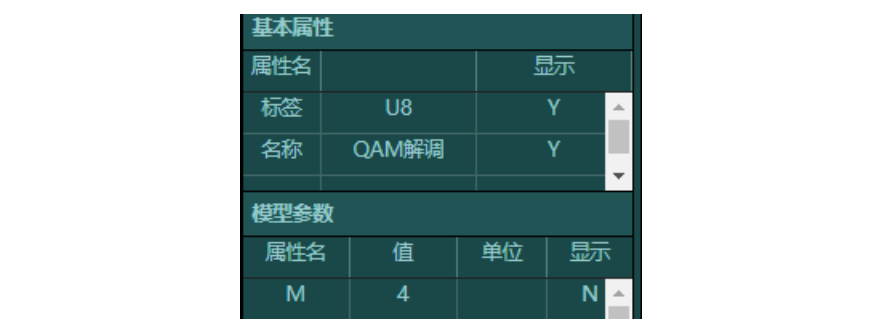
QAM 解调模块
四、 实验方法与步骤要求
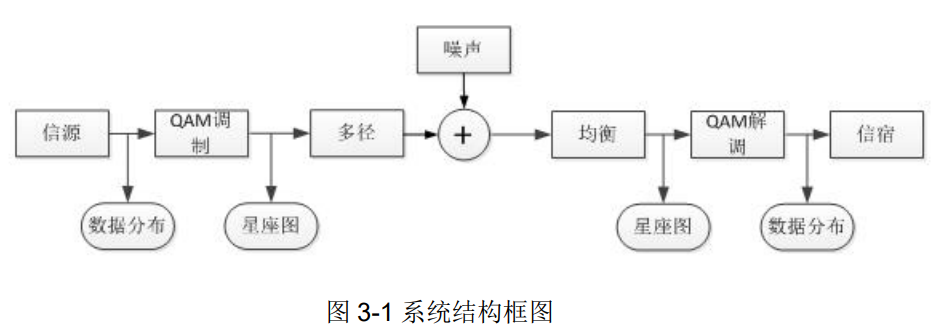
1、如下图 3-1 所示搭建仿真实验模型:对比分析经过噪声、多径干扰、迫零均衡处理等过程前后 QAM 调制星座图发生的变化。
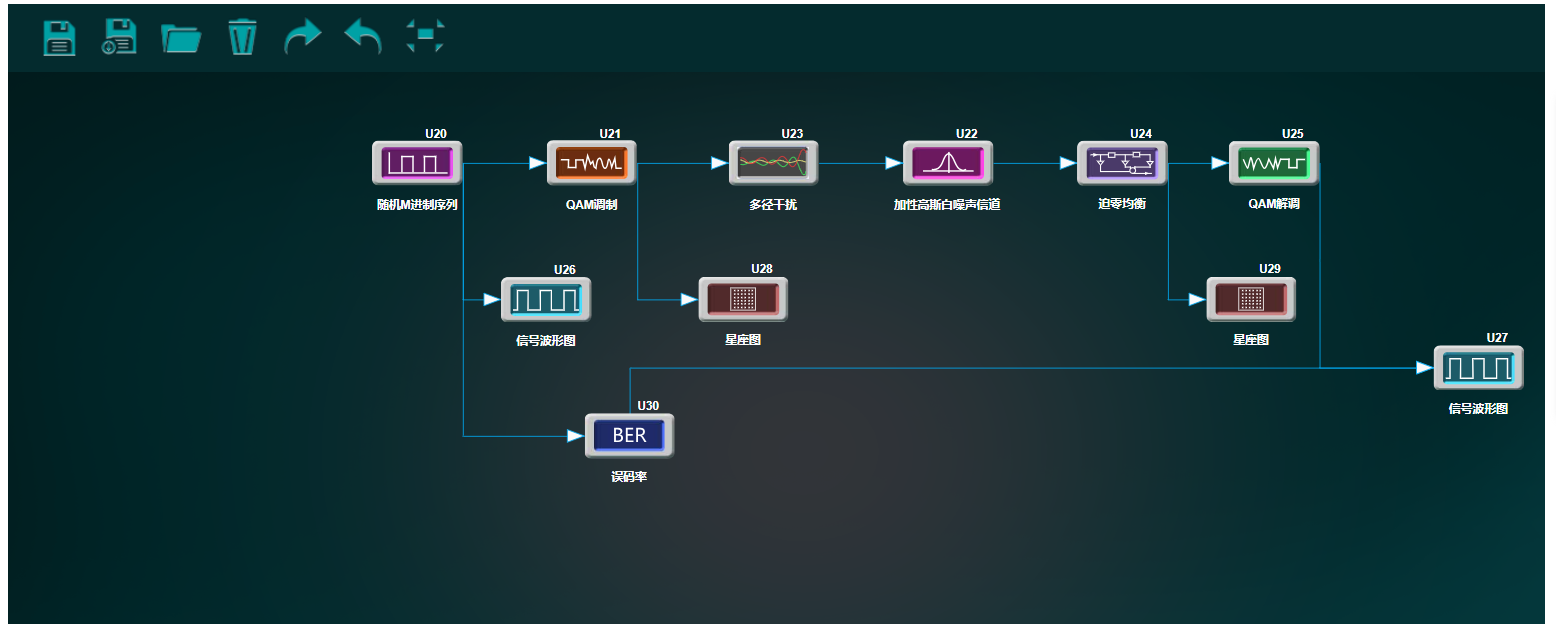
系统整体如下图所示:
2、设置器材参数:
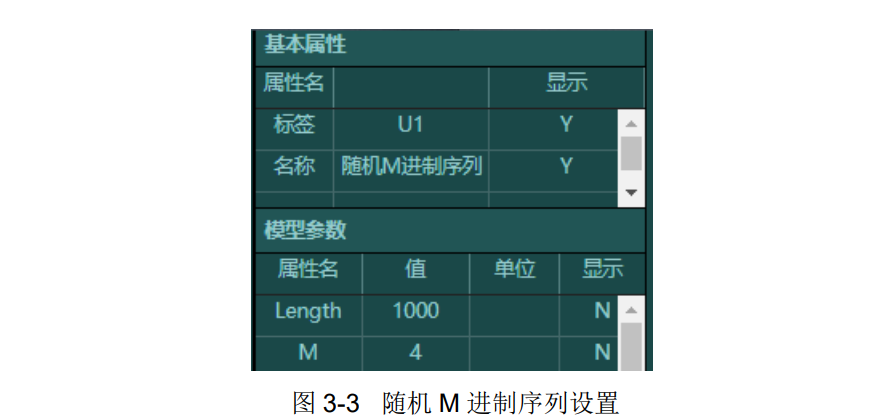
a.随机 M 进制序列模块:序列数据的长度设置为 1000,序列数据的进制数设置为 4;
b.QAM 调制模块:输入数据的进制数设置为 4;

c.加性高斯白噪声信道模块:设置信噪比为30dB;

d.多径干扰模块:多径信道的冲激响应设置为[0.02 0.05 0.1 -0.2 1 -0.2 0.1 0.05 0.02];

e.迫零均衡模块:信道的冲激响应设置为[0.02 0.05 0.1 -0.2 1 -
0.2 0.1 0.05 0.02};均衡器抽头数目设置为 30;
f.QAM 解调模块:输入数据的进制数设置为 4;
g.星座图:数据长度设置为 1000,图像宽度设置为 10,图像高度设置为 8;

3、点击按钮运行仿真,观察输出波形及误码率统计。
4、将高斯噪声模块的输入信噪比设置为 15dB,其余不变,运行仿真,观察输出波形及误码率统计。
5、将随机 M 进制序列、QAM 调制、QAM 解调等模块的数据进制数改为 16,其余不变,运行仿真,观察输出波形及误码率统计。
6、将随机 M 进制序列、QAM 调制、QAM 解调等模块的数据进制数改为 64,其余不变,运行仿真,观察输出波形及误码率统计。
五、 实验结果与结论
实验结果信号分布如下所示:
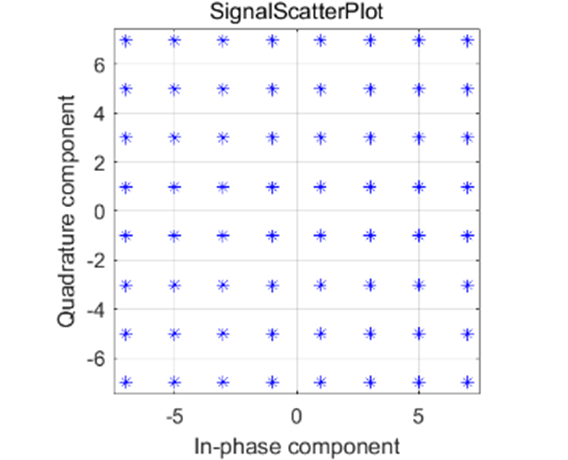
由图 3-11 可以知道,64QAM 调制同时利用信号的相位和幅度变量来传递数据,一个符号可以携带 6bits 信息。而不采用调制时,一个符号仅能传递1bit 信息。当采用了QAM调制时,信道得到了充分了利用。我们可以观察到输出误码率为0且过信道后星座图星座点分明,没有交叠现象,说明信息传输正确。
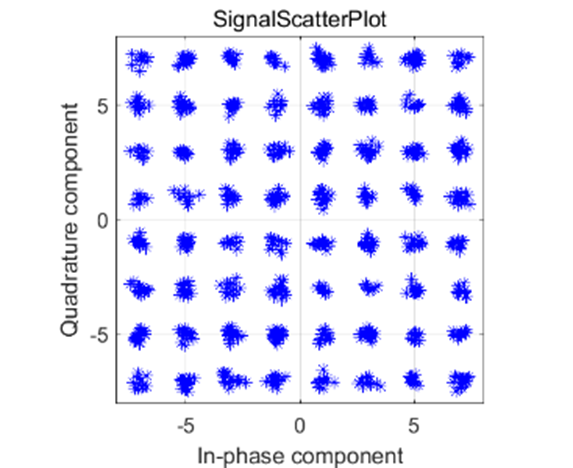
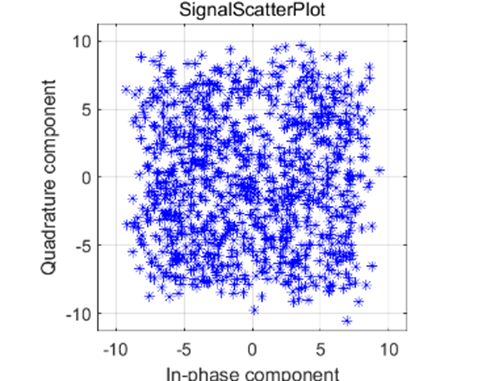
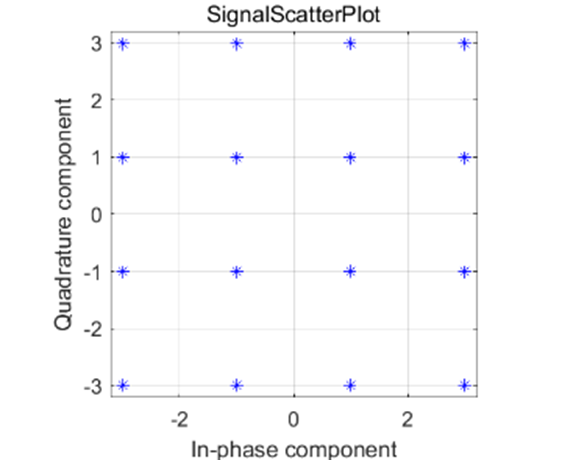
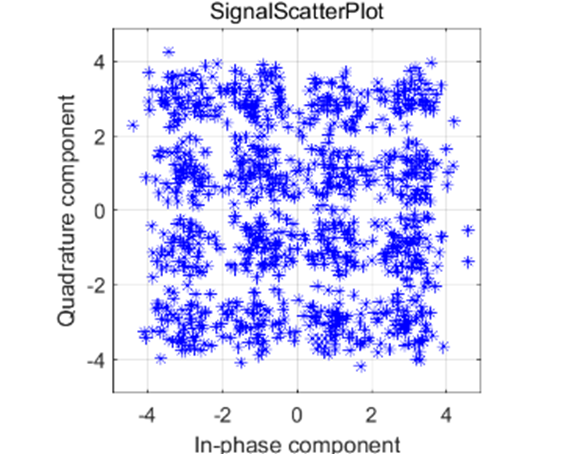

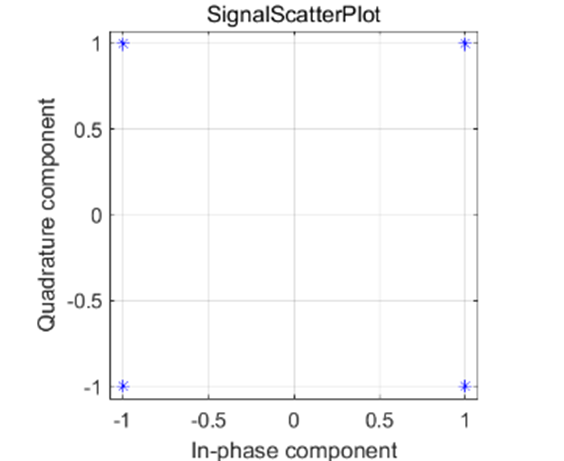
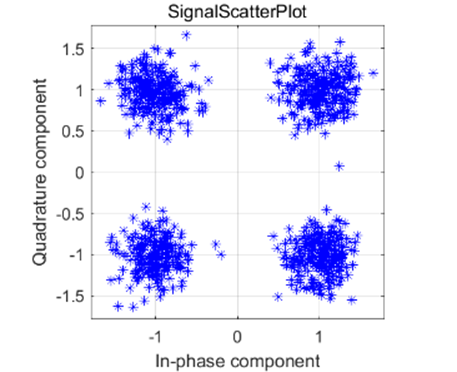
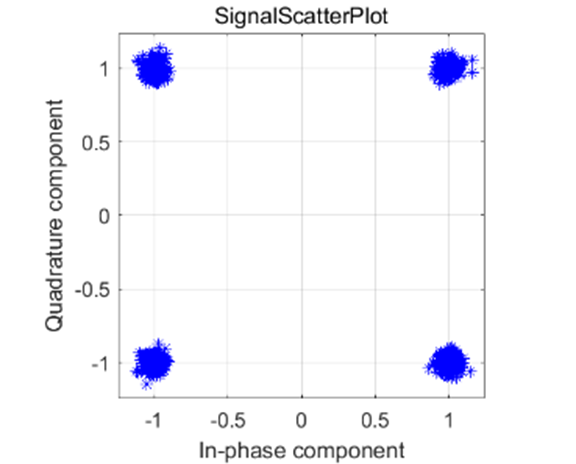
由上面的图我们可以看出,在相同的信噪比下,64QAM 星座图散乱严重,误码率为1.13*10^{-1},数据无法正常解调;16QAM 星座图部分发散,误码率为5.0*10^{-3},数据勉强能够解调;QPSK 星座图较聚合,误码率为7.5*10^{-5},数据解调正确。由以上我们可以知道虽然高阶调制可以提高信道的利用率,但是其对噪声和多径变得更加敏感。


